仮想通貨の自動売買ツールをPythonで自作する　移動平均線について

移動平均線とは？

　移動平均線とは、本来ローソク足のみで表される株価や、仮想通貨のチャート画面に描くグラフの事です。

　ローソク足だけだと読みにくいので、チャートを見ながらのトレードを行う際には、移動平均線を表示し、読みやすくしてから今後の値動きを予測します。

　自動売買ツールでも、移動平均線を使用して売買のタイミングを測るものが多いと思われます。

　私が自作した仮想通貨の自動売買ツールも、APIを使用して取引所からローソク足データを取得し、それを使用して移動平均線を算出して、売買タイミングを見極めています。

　この記事で自動売買ツールを運用するまでの7ステップをまとめてあります。

あわせて読みたい

仮想通貨の自動売買ツールをPythonで自作　作成～運用開始までの7ステップ 仮想通貨の自動売買ツールを作成から運用まで行うまでを６ステップでまとめました。

移動平均線の種類

　仮想通貨に限らず株やFXなどで、トレードの指標として使用されている移動平均線は主に3種類あります。

単純移動平均線（SMA）とは

　単純移動平均線は「SMA」とも呼ばれる移動平均線です。決められた期間内にある全データの平均を求めるというシンプルな仕組みなので、簡単に計算を行うことが可能です。

　以下の２つの平均線よりも、直近の値動きに対する反応が鈍いですが、大きなトレンドの波を見るのに使用されることが多いです。

加重移動平均線（WMA）とは

　加重移動平均線は「WMA」とも呼ばれる移動平均線です。単純移動平均線とは違い最新のデータになるに連れて、データに重み(Weight)を付けて計算を行うため、単純移動平均線よりも直近の値動きに対して早く反応をします。

指数平滑移動平均線（EMA）とは

　指数平滑移動平均線は「EMA」とも呼ばれる移動平均線です。加重移動平均線と同じで最新のデータに重きを置き、過去のデータ程影響度が減っていく平均方法になります。ですが、加重移動平均線よりは直近の値動きに対して反応が遅いという特徴があります。

　ちなみに、過去のデータの影響度が指数関数的に減少していくことから、指数平滑移動平均線と呼ばれるようです。

移動平均線3種類のメリット・デメリット

単純移動平均線のメリット・デメリット

単純移動平均線のメリット

計算が簡単

　名前の通り単純に決めた期間のデータの平均を出す方法のため、計算がシンプルで簡単です。

直近の値動きに反応し過ぎない

　期間内の全データを平等に扱うので、直近で高騰又は暴落が起きたとしても単純移動平均線は大きく反応しないため、グラフは緩やかなカーブを描きます。

単純移動平均線のデメリット

反応が鈍いため、相場の動きよりも遅れる

メリットに相反する事ですが、直近の値動きに大きく影響されないので、相場の動きよりも一足遅れて動きます。

そのため、単純移動平均線だけを使用していると売買のタイミングが遅れてしまう可能性が高いです。

加重移動平均線のメリット・デメリット

加重移動平均線のメリット

計算が比較的簡単

　単純移動平均線よりもデータに重さを乗せる手順がありますので、計算の手間が少し増えますが計算式自体はそれほど難しくありません。

直近の値動きに素早く反応してくれる

　直近のデータになるほど大きな重さを一定に乗せるので、単純移動平均線よりも最近のトレンドを早く捉える事ができます。

加重移動平均線のデメリット

ダマシが多くなる

　メリットで挙げたように、直近の値動きに素早く反応してくれるのですが、それが仇となり上昇トレンドが始まったと思ったら、直ぐに下がってしまう「ダマシ」が多くなります。

指数平滑移動平均線のメリット・デメリット

指数平滑移動平均線のメリット

直近の値動きに素早く反応してくれる

　加重移動平均線のメリットと同様ですが、指数平滑移動平均線も最近の値に重きを置くため、直近の値動きに対して素早く反応を示してくれます。

　ただ、加重移動平均線と比べると反応速度は遅れます。

MACDなどの指標にも使われている

　MACDというトレンド転換を予測する指標があるのですが、その計算に指数平滑移動平均線が使用されています。

　そのため、この平均線がどのようなものかをわかっておくと、MACDの仕組みもある程度わかるようになります。

指数平滑移動平均線のデメリット

計算が少し複雑

　上記の２つの移動平均線と比べて、少し計算方法がわかりにくいです。

詳しい計算方法は後述しますが、データの平均を求めるような方法ではないので理解に時間がかかりました。（私だけかもしれませんが…）

ダマシが多くなる

　加重移動平均線と同じように、直近のデータに対して反応が素早いので、やはりダマシが発生しやすいです。

移動平均線３種類を実際にグラフで比較

　実際に仮想通貨のチャートへ、３種類の移動平均線を使用して並べてみました。（画面はビットバンクを利用しています）

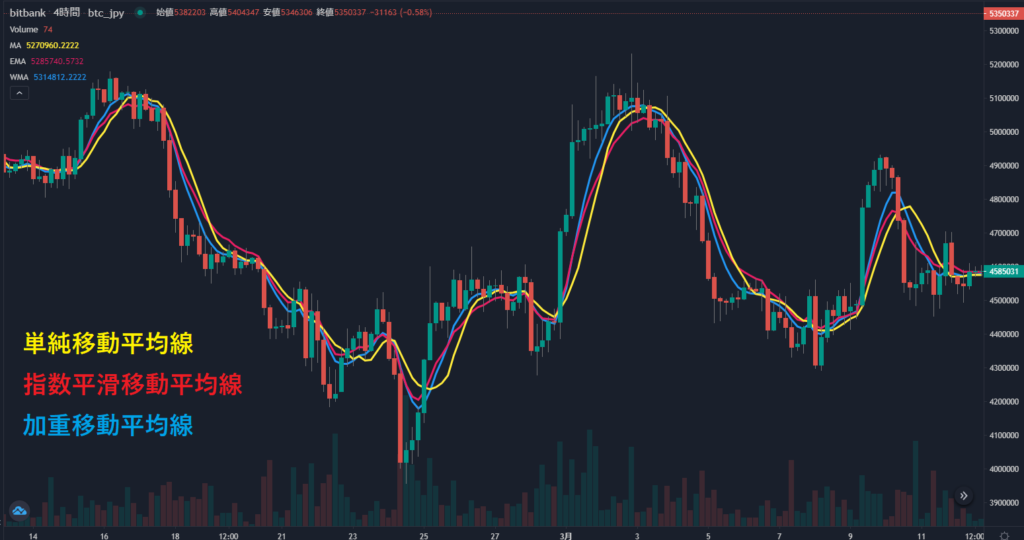
　元は同じデータから作っているのに、それぞれグラフがズレていますね。

　単純移動平均線は、他の２本に比べて一歩遅れて山や谷ができているのがわかります。

　加重移動平均線と指数平滑移動平均線では、グラフの山と谷の出現がほとんど同じタイミングに見えますが、加重移動平均線の方がよりローソク足の動きに沿ってグラフが引かれているように見えます。

移動平均線の計算方法

　３種類の移動平均線の計算方法を紹介します。ここでは日足のデータを使用して、期間を５日の移動平均を求める事とします。

単純移動平均線の計算方法

　単純移動平均線の計算方法は前述した通り、設定した期間の全データの平均ですので、データの値を全て足し、そのデータ数で割ります。小学校で習う「平均」の求め方と同じ計算方法です。

　３種類の中で、最もシンプルで分かりやすい計算方法です。

加重移動平均線の計算方法

　加重移動平均線の計算方法は、基本的に単純移動平均線と同じように見えますがデータに「重み」を載せて計算を行います。

　直近のデータ程、大きな重みを載せるため、最新のデータに素早く反応した値が出てきます。

指数平滑移動平均線の計算方法

　指数平滑移動平均線は以下のように、３つの手順を踏んで求められます。

　他2つと大きく違う点として、平滑化係数という値の計算が必要です。

　初回データのみ単純移動平均で求め、２回目以降はこの指数平滑移動平均で求められた値を使用して計算を行っていきます。

　古いデータの重要性は徐々に減っていく仕組みですが、加重移動平均線のように決まった重みを載せる方法ではないので、加重移動平均線よりも遅い反応となります。

移動平均線３種類をPythonで実装　コピペ可能

　それぞれの移動平均線をPythonコードで紹介します。

　関数として記載しますので、コピペでそのまま使えるはずです。引数にデータ(List型)と、求めたい移動平均線の期間(int型)を渡せば移動平均のデータがList型で返ってきます。（間違ってたらごめんなさい）

単純移動平均線をPythonで実装

def smaCalculation(datalist,periods):
    #datalist = 元データのリスト
    #periods = 設定期間
    smaData = []    #計算結果格納用List
    sum = 0         #足し算結果の格納用変数
    for i in range(len(datalist)-periods + 1):
        for j in range(periods):
            sum = datalist[i+j] + sum
        smaData.append(sum / periods)
        sum = 0
    return smaData

加重移動平均線をPythonで実装

def wmaCalculation(datalist,periods):
    #datalist = 元データのリスト
    #periods = 設定期間
    wmaData = []    #計算結果格納用List
    sum = 0         #足し算結果の格納用変数
    weightSum = periods * (periods + 1) * 0.5  #重さの和
    for i in range(len(datalist)-periods + 1):
        for j in range(periods):
            sum = datalist[i+j]*(j+1) + sum
        wmaData.append(sum / weightSum)
        sum = 0
    return wmaData

指数平滑移動平均線をPythonで実装

def emaCalculation(datalist,periods):
    emaData = []            #計算結果格納用List
    a = 2 / (periods + 1)   #平滑化係数を計算
    sum = 0                 #足し算結果の格納用変数
    for i in range(periods):
        sum = datalist[i] + sum
    emaData.append(sum / periods)    #初回データを計算し格納
    #初回データ以降を計算していく
    for i in range(len(datalist) - periods-1):
        emaData.append(emaData[i] + a * (datalist[len(datalist) - periods + i] - emaData[i]))

    return emaData

移動平均線のまとめ

　各種移動平均線によってそれぞれの特徴があり、メリット・デメリットが存在しているため、一概にどれが正解と言うのはありません。適材適所で使い分けていく必要があります。

　手動でのトレードではもちろんですが、移動平均線を利用する自動売買ツールを自作する際には、それぞれの特徴を理解して最適なものを選びましょう。

あわせて読みたい

ビットバンクの口座開設方法【けっこう簡単】 仮想通貨の取引所であるbitbank（ビットバンク）の口座開設方法を解説した記事です。通販サイトなどに登録したことがある方なら、簡単に開設できます。